Score-based Generative Modeling of Graphs via the System of Stochastic Differential Equations
Score-based generative models have achieved strong results in image and molecular generation, but applying them to graph-structured data remains challenging due to the complex interplay between node features and graph topology. In this blog, we explore GDSS (Graph Diffusion via the System of Stochastic differential equations), a model that tackles this problem by jointly modeling the evolution of node attributes and adjacency matrices through a system of coupled stochastic differential equations. Using a permutation-equivariant graph neural network and score matching, GDSS generates graphs that maintain both structural validity and semantic coherence.
Introduction: Why Graph Generation Matters
Graphs are fundamental to representing structured relationships in various domains, such as molecular structures in drug discovery
While traditional generative models, such as VAEs, GANs, and autoregressive models, have achieved limited success when applied to graphs due to these complexities, recent advancements in score-based generative modeling
Limitations of Existing Methods
Autoregressive models like GraphRNN
VAE-based models such as GraphVAE
GAN-based models like MolGAN
Flow and early diffusion models like GraphAF
EDP-GNN
While graph generation aims to synthesize graphs that closely match the distribution of observed data, these limitations highlight the need for a model that can jointly model nodes and edges on continuous-time domain, respect graph symmetries, and scale with complexity: and GDSS meets this need.
How GDSS Works
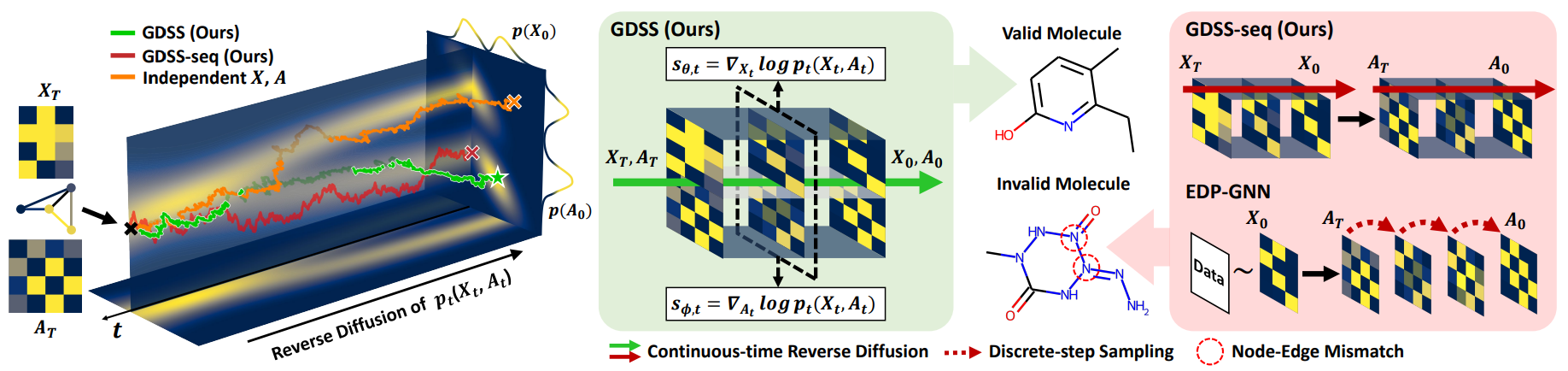
GDSS tackles these limitations by proposing a (1) scored-based graph generation framework (2) on a continuous-time domain that can (3) generate both the node features and the adjacency matrix.
During training, the model learns two score functions that approximate the gradients of the log-density of the noisy data with respect to node features and edges. A permutation-equivariant score based model learns these scores, capturing correlations between structure and semantics. This design allows GDSS to simulate the reverse-time SDEs and sample realistic graphs from noise, achieving state-of-the-art performance on both synthetic and molecular graph benchmarks.
An overview of GDSS’s process is shown below.
0. Data Representation
To start with, GDSS operates on undirected graphs with node features, represented as
\[G = (X, A): X \in \mathbb{R}^{N \times F}, \quad A \in \mathbb{R}^{N \times N}\]where $X$ is the node feature matrix for $N$ nodes, each with dimension $F$ features and $A$ is the symmetric adjacency matrix.
1. Forward Diffusion via Coupled SDEs
To model the dependency between $X$ and $A$, GDSS formulates a forward diffusion process of graphs that transforms both of them to a simple noise distribution. The forward process \({G_t = (X_t,A_t)}, t∈[0,T]\) is defined by two independent SDEs, as shown below:
\[d\mathbf{G}_t = \mathbf{f}_t(\mathbf{G}_t) \, dt + \mathbf{g}_t(\mathbf{G}_t) \, d\mathbf{w}, \quad \mathbf{G}_0 \sim p_{\text{data}}\]where $\mathbf{f}_t$ is the linear draft coefficient, $\mathbf{g}_t$ is the diffusion coefficient and $w$ is standard Wiener processes. $\mathbf{f}_t$ and $\mathbf{g}_t$ are chosen such that at the terminal time horizon $T$, the diffused sample $G_T$ approximately follows a prior distribution that has a tractable form to efficiently generate the samples, such as Gaussian distribution. To make it simpler, \(\mathbf{g}_t(\mathbf{G}_t)\) is chosen to be a scalar function $g_t$.
2. Reverse Process with Learned Score Functions
To generate graphs that follow the data distribution, GDSS start from samples of the prior distribution and leverage the following g reverse-time SDE
where $p_t$ is the marginal distribution under the forward diffusion process at time \(t\), \(\bar{\mathbf{w}}\) is a reverse-time standard Wiener process, and \(d\bar{t}\) is an infinitesimal negative time step.
For efficient computing of \(\nabla_{G_t} \log p_t(G_t)\), GDSS utilizes below equations, which operate the same function as above equation. This is a novel approach that interprets the diffusion of a graph as the diffusion of each component that are interrelated through time.
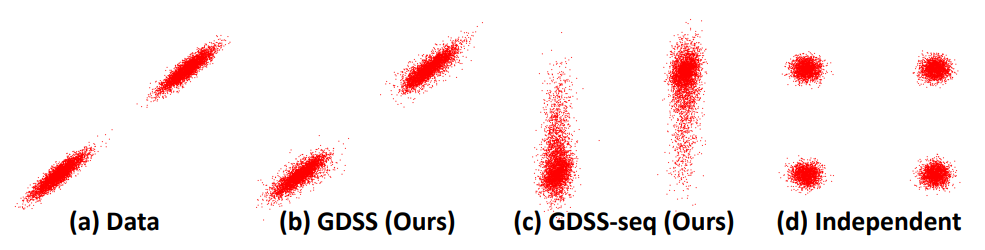
\[dX_t = [f_{1, t}(X_t)-g_{1, t}^2 \nabla_{X_t} \log p_t(X_t, A_t)] d\bar{t} + g_{1, t} d\bar{\mathbf{w}}_1\] \[dA_t = [f_{2, t}(A_t)-g_{2, t}^2 \nabla_{A_t} \log p_t(X_t, A_t)] d\bar{t} + g_{2, t} d\bar{\mathbf{w}}_2\]The key property of GDSS is that the diffusion processes in the system are dependent on each other, as shown in the partial score functions, \(\nabla_{X_t} \log p_t(X_t, A_t)\) and \(\nabla_{A_t} \log p_t(X_t, A_t)\). To show the importance of modeling the dependency, Figure 2 compares the generated samples with the data distribution as bivaraite Gaussian mixture, which shows that GDSS successfully handles correlation of two variables while others ((c) GDSS-seq : that generates \(X\) and \(A\) sequentially and not simultaneously or (d) that ignores the diffusion process of \(X\)) can’t.
Now, since the exact score functions $\nabla_{X_t} \log p_t$ and $\nabla_{A_t} \log p_t$ are unknown, GDSS learns parameterized approximations as follow:
\(s_{\theta, t}(G_t) \approx \nabla_{X_t} \log p_t(G_t), \quad s_A(\phi, t) \approx \nabla_{A_t} \log p_t(G_t)\).
Considering that the score-based models should be trained to minimize the distance to the corresponding ground-truth partial scores, GDSS utilizes a novel objectives that generalize the score matching
However, in above equation, the ground-truth partial scores are not accessible, so GDSS denoises score matching to the partial scores, as shown below:
\[\min*{\theta} \, \mathbb{E}\_t \left\{ \lambda_1(t) \, \mathbb{E}*{G*0} \, \mathbb{E}*{G*t|G_0} \left\| s*{\theta,t}(G*t) - \nabla*{X*t} \log p*{0t}(G_t | G_0) \right\|\_2^2 \right\}\] \[\min*{\phi} \, \mathbb{E}\_t \left\{ \lambda_2(t) \, \mathbb{E}*{G*0} \, \mathbb{E}*{G*t|G_0} \left\| s*{\phi,t}(G*t) - \nabla*{A*t} \log p*{0t}(G_t | G_0) \right\|\_2^2 \right\}\]Furthermore, since the drift coefficient of the forward diffusion process is linear as shown below,
\[d\mathbf{G}_t = \mathbf{f}\_t(\mathbf{G}\_t) \, dt + \mathbf{g}\_t(\mathbf{G}\_t) \, d\mathbf{w}, \quad \mathbf{G}\_0 \sim p_{\text{data}}\]we can get
\[p*{0t}(G_t \mid G_0) = p*{0t}(X*t \mid X_0) \cdot p*{0t}(A_t \mid A_0)\]As a result, the final equation can be summarized as below, with more details for the derivations found in GDSS
Now, it is important to note that estimating the partial scores of GDSS is different from estimating marginal scores $$
\nabla{X_t} \log p_t(X_t) \quad \text{or} \quad \nabla{A_t} \log p_t(A_t)
\[used in previous score-based generative models because GDSS requires capturing the dependency between node features $X_t$ and adjacency matrices $A_t$ through their joint probability over time. Since above training objectives enable effective estimation of these partial scores, the next step is to design model architectures capable of learning them. ### 3. Permuation-equivariant Score-based Model <!-- GDSS employs a single Equivariant Graph Neural Network (EGNN) to learn both score functions jointly. This ensures (1) permutation equivariance, so the node order does not affect the output, (2) joint modeling, so that the node features and adjacency are processed together. --> For this, GDSS propose two neural architectures based on Graph Neural Networks (GNNs). <!-- To effectively learn the partial scores in GDSS, we need score networks that can capture the intricate dependencies between node features\]X_t
\[and adjacency structures\]A_t.
\[GDSS propose two neural architectures based on Graph Neural Networks (GNNs) that are tailored to this goal. --> For the adjacency score, the model\]s_{\phi,t}(G_t)
\[estimates the gradient\]\nabla_{A_t} \log p_t(X_t, A_t).
\[This is done by graph multi-head (GMH) attention, which helps identify key relational patterns between nodes, along with higher-order adjacency matrices to account for long-range interactions. These representations are then passed through a multi-layer perceptron (MLP) to produce the final score. For the node feature score, the model\]s_{\theta,t}(G_t)
\[targets\]\nabla_{X_t} \log p_t(X_t, A_t).
\[It stacks multiple GNN layers to compute contextual node embeddings from the adjacency matrix, which are again aggregated via an MLP to form the score estimate. Importantly, both models incorporate time conditioning by scaling their outputs with the standard deviation of the diffusion process at time\]t,
\[following previous work<d-cite key="song2020generativemodelingestimatinggradients"></d-cite>. Because GNNs and GMH layers are permutation-equivariant, the resulting score functions preserve the permutation invariance of graph distributions, which is an essential property for meaningful graph generation. ### 4. Solving the Reverse Time SDE System with S4 Once GDSS learns the partial scores for nodes and edges, the next challenge is generating graphs by solving the **reverse-time diffusion process**:\]\begin{cases} \mathrm{d}\mathbf{X}t = f{1,t}(\mathbf{X}t)\,\mathrm{d}t + g{1,t}\,\mathrm{d}\bar{\mathbf{w}}1 \underbrace{-\, g{1,t}^2\, s{\theta,t}(\mathbf{X}_t, \mathbf{A}_t)\,\mathrm{d}t}{\textbf{S}}
\mathrm{d}\mathbf{A}t = f{2,t}(\mathbf{A}t)\,\mathrm{d}t + g{2,t}\,\mathrm{d}\bar{\mathbf{w}}2 \underbrace{-\, g{2,t}^2\, s{\phi,t}(\mathbf{X}_t, \mathbf{A}_t)\,\mathrm{d}t}{\textbf{S}} \end{cases} \quad \underbrace{\text{First two terms}}_{\textbf{F}}
$$
These coupled SDEs are not trivial to solve due to the tight interdependence between $X_t$ and $A_t$. To address this, GDSS introduces S4 (Symmetric Splitting for Systems of SDEs), a new solver that balances accuracy and efficiency, which is inspired from previous works
Each reverse-time step is decomposed into three phases:
- Score Computation: Estimate partial scores \(s_{\theta,t}\) and \(s_{\phi,t}\) using the trained networks.
- Correction: Use a Langevin MCMC step to refine the current state \(G_t\), ensuring alignment with the learned score.
- Prediction: Use the Fokker-Planck operators for both drift (F) and score (S) terms to evolve the graph state backward. This is done via the Trotter splitting scheme:
where the F-term is sampled from the known forward diffusion transition, and the S-term is approximated using a simple Euler method. Further details regarding the derivations can be found in
By cleverly reusing the same precomputed scores in both the correction and prediction steps, S4 achieves high efficiency, and compared to PC samplers, S4 cuts the number of score network calls in half, saving compute without sacrificing quality.
Importantly, S4 is also generalizable: it can handle systems involving both Variance Exploding (VE) and Variance Preserving (VP) SDEs
Experimental Results
Generic Graph Generation
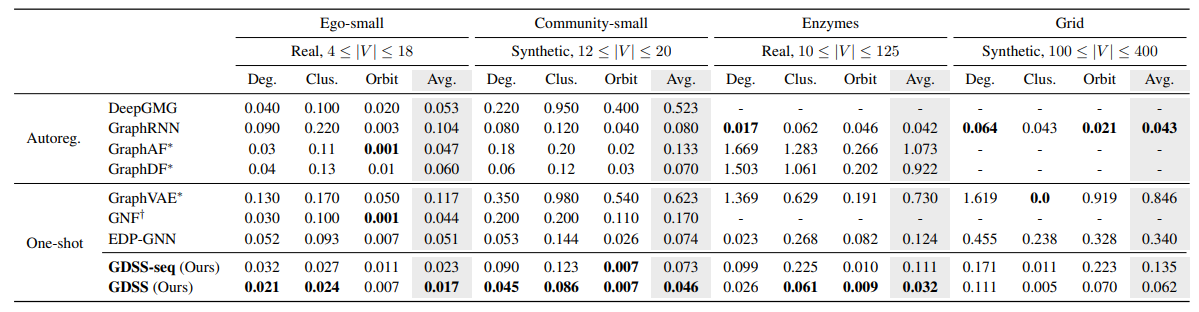
In Table 1, GDSS demonstrates significant improvements over previous one-shot graph generative models, including the prior score-based method EDP-GNN. GDSS not only surpasses all one-shot baselines but also outperforms most autoregressive models, which are generally more powerful but computationally expensive.
Especially, in Grid dataset, while most models struggle, GDSS achieves results that are on par with GraphRNN, a strong autoregressive baseline. In contrast, EDP-GNN fails entirely on large graphs, confirming the limitations of its discrete, adjacency-only generation scheme.
Now, a natural concern when estimating the joint partial score $$
\nabla_{A_t} \log p_t(X_t, A_t)
\[is that it might be significantly harder than estimating simpler marginal-like scores, such as\]\nabla_{A_t} \log p_t(X_0, A_t)
\[which ignore the time-evolving dependency between node features and edges. Surprisingly, the empirical findings suggest the opposite, as shown in Figure 3. <figure> <picture> <source class="responsive-img-srcset" media="(max-width: 480px)" srcset="/assets/img/2025-04-28-paper-1/fig1-480.webp" /> <source class="responsive-img-srcset" media="(max-width: 800px)" srcset="/assets/img/2025-04-28-paper-1/fig1-800.webp" /> <source class="responsive-img-srcset" media="(max-width: 1400px)" srcset="/assets/img/2025-04-28-paper-1/fig1-1400.webp" /> <!-- Fallback to the original file --> <img src="/assets/img/2025-04-28-paper-1/fig1.png" width="auto" height="auto" onerror="this.onerror=null; $('.responsive-img-srcset').remove();" /> </picture> </figure> <div class="caption"> <a href="https://arxiv.org/abs/2202.02514" target="_blank">Figure 3: Complexity of the score-based models.</a> </div> 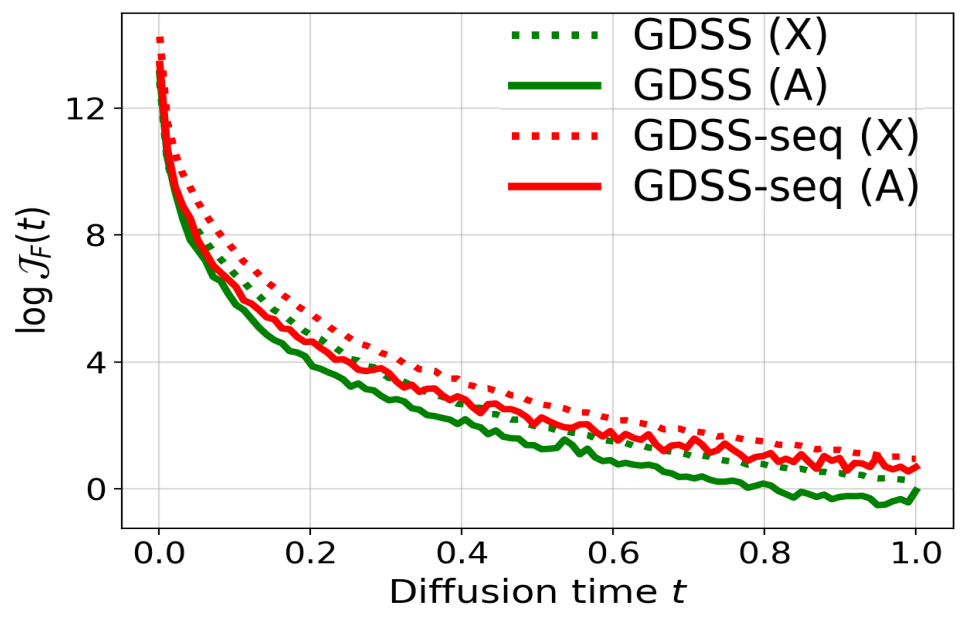To investigate this, the **complexity of the score-based models** is measured using the **squared Frobenius norm of their Jacobians**, denoted \( J_F(t) \). GDSS, which learns joint partial scores, is compred to to GDSS-seq, a variant that simplifies the dependency assumptions. As shown in Figure 3, GDSS actually exhibits **lower model complexity** than GDSS-seq when trained on the Ego-small dataset. This holds for both:\]\nabla{A_t} \log p_t(X_t, A_t) \quad \text{and} \quad \nabla{X_t} \log p_t(X_t, A_t)
$$
This counterintuitive result highlights a key strength of GDSS: by modeling the true node-edge dependency, the model not only gains better generative performance (as shown in Table 1), but also becomes easier to train in terms of optimization complexity. These findings further validate the design of GDSS as a principled and scalable graph generation framework.
Molecule Generation Performance and Efficiency
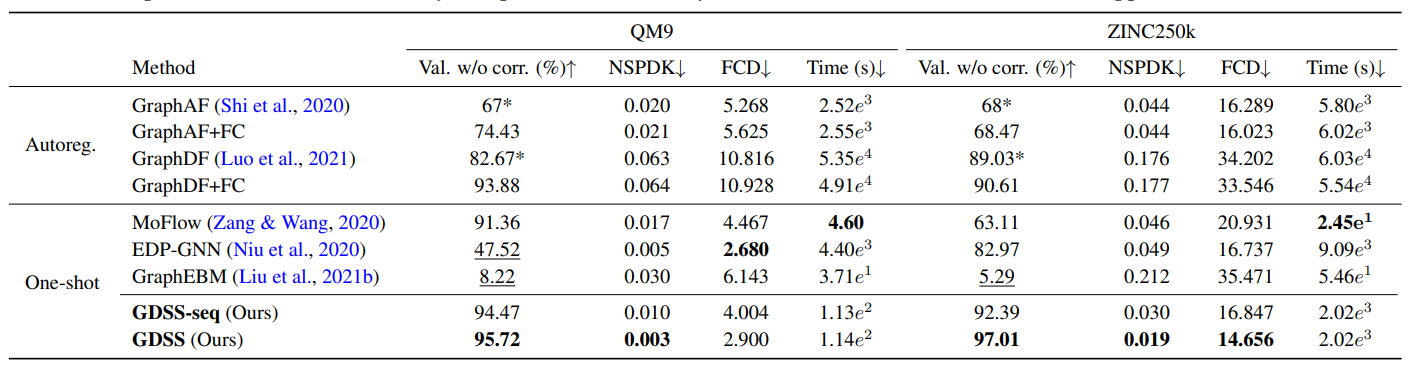
GDSS shows strong results in the task of molecular graph generation. As shown in Table 2, it achieves the highest validity among all methods without relying on post-hoc valency correction. This indicates that GDSS effectively learns the chemical valency rules, which fundamentally rely on modeling the relationship between atoms (nodes) and bonds (edges).
GDSS also significantly outperforms all baselines in NSPDK MMD, and most in Fréchet ChemNet Distance (FCD), demonstrating that the generated molecules are not only structurally realistic in graph space but also chemically plausible in feature space. This shows GDSS’s ability to model complex joint distributions of molecules with diverse node and edge types.
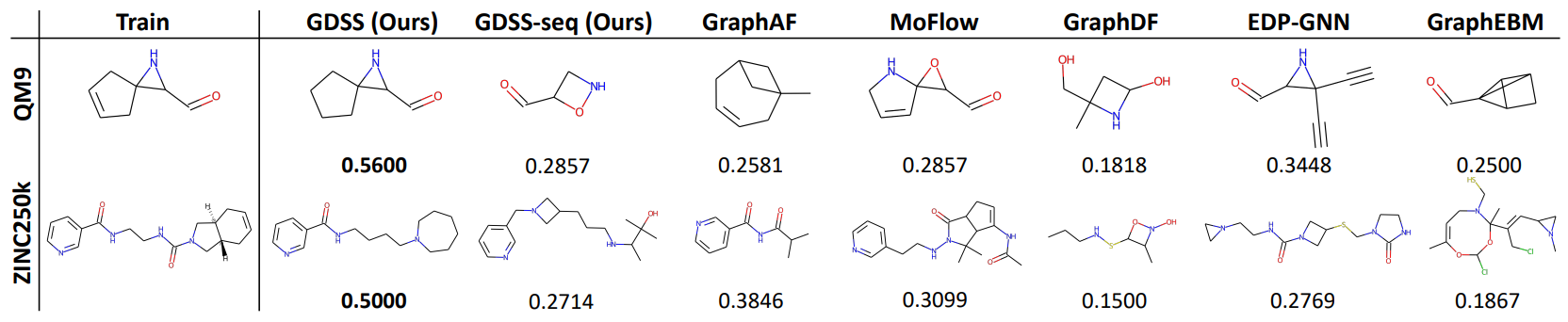
Visualizations in Figure 4 further emphasizes this result: molecules generated by GDSS often share large substructures with those from the training set. In contrast, baseline methods frequently produce molecules with less resemblance or completely unrelated structures, highlighting GDSS’s superior generative fidelity.
Beyond quality, GDSS is also highly efficient, as shown in Table 2. On the QM9 dataset, GDSS achieves a 450× speed-up in generation time compared to GraphDF, one of the strongest autoregressive baselines. This efficiency stems from GDSS’s continuous-time diffusion framework, which replaces costly sequential sampling with a more scalable reverse-time SDE simulation.
Additionally, both GDSS and its variant GDSS-seq outperform EDP-GNN in generation speed. This further validates that modeling graph transformation as a continuous diffusion process is not only more expressive but also much more practical than discrete-step perturbation methods.
Ablation Studies
Why Modeling Node-Edge Dependency Matters
To assess the importance of capturing the dependency between node features and edges, GDSS is compared with GDSS-seq, where GDSS models the joint dependency between $X$ and $A$, while GDSS-seq assumes that $A$ depends only on $X$, simplifying the reverse SDE system. This subtle design choice turns out to be crucial.
Across all benchmarks in Table 1 (generic graphs) and Table 2 (molecules), GDSS consistently outperforms GDSS-seq in every metric. The results clearly demonstrate that accurately modeling the graph distribution requires learning both node and edge interactions through time, rather than treating them as partially independent.
For molecule generation in particular, the benefit is measurable in terms of chemical validity. GDSS achieves higher validity scores without needing valency correction, directly showing that it better captures the structure–function relationship between atoms and bonds.
These findings confirm that the proposed system of SDEs—where the partial scores
\[\nabla\_{X_t} \log p_t(X_t, A_t)\]and
\[\nabla\_{A_t} \log p_t(X_t, A_t)\]are co-trained—provides a more faithful and powerful approach to generative graph modeling.
Significance of S4 Solver
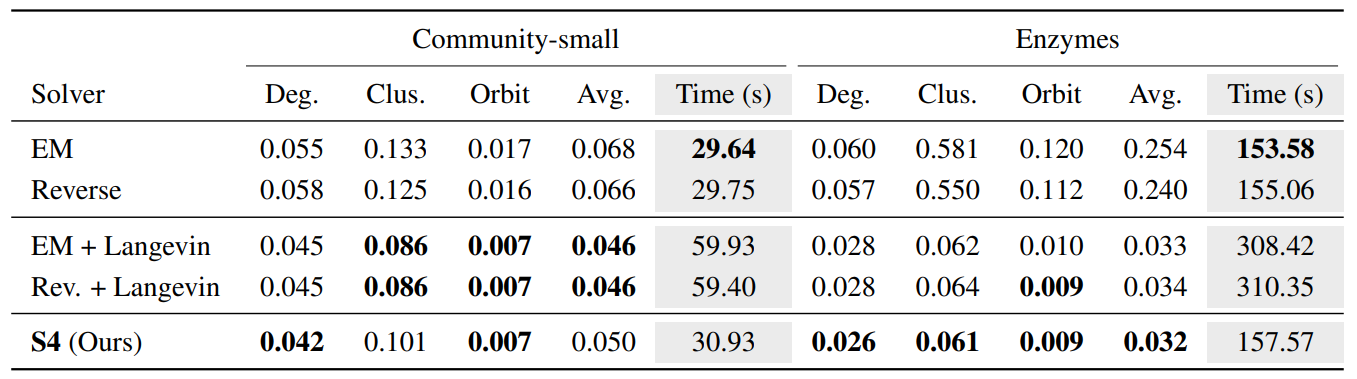
As shown in Table 3, S4 significantly outperforms both Euler–Maruyama (EM) and Reverse sampler, which are simple baseline solvers for reverse-time diffusion, validating the advantage of including both prediction and correction steps. More impressively, despite using half the number of score network evaluations, S4 also outperforms the PC samplers, a more advanced methods using Langevin MCMC for correction.
This efficiency stems from S4’s use of symmetric splitting and score reuse, which allow it to maintain high sampling accuracy while dramatically reducing computational overhead. Since score-based model evaluations dominate the cost of solving stochastic differential equations (SDEs), this reduction is critical for scaling to large or complex graphs. By combining accuracy, efficiency, and generality, S4 becomes a powerful and practical solver for simulating the reverse diffusion process in GDSS.
Final Thoughts
GDSS redefines the paradigm of graph generation by enabling the joint, continuous, and permutation-invariant synthesis of both graph structure and semantic node features. It uses the stochastic differential equations (SDEs) and the score-based diffusion modeling to navigate the complex space of structured data. By coupling feature-edge diffusion dynamics and employing equivariant GNN-based score estimators, GDSS establishes a framework for generating valid, diverse, and semantically coherent graphs, contributing to areas including, molecular modeling, synthetic biology, and network science.
Key Takeaways
-
Unified Joint Modeling By treating the adjacency matrix and node features as co-evolving under a system of SDEs, this work overcomes the typical fragmentation in graph generation. It significantly improves structural-semantic alignment, which is crucial for tasks like molecular graph synthesis.
-
Permutation-Invariant Score Learning Leveraging permutation-equivariant score-based model ensures that the model respects the graph’s inherent symmetries, meaning that the node permutations do not affect the outcome, addressing a key limitation in many autoregressive approaches.
-
Continuous and Flexible Framework Diffusion-based generative modeling offers continuous-time flexibility and avoids common drawbacks like mode collapse seen in GANs and VAEs. It is especially suited for high-dimensional, sparse, and structured graph data.
-
Empirical Strength The GDSS model achieves state-of-the-art results on graph generation tasks, outperforming both one-shot and autoregressive baselines on benchmarks like QM9 and ZINC250k in terms of Validity (no correction), NSPDK MMD (structural fidelity), FCD (chemical distribution closeness). Among the SDE types, VE-SDE paired with the efficient S4 solver delivers the best stability, quality, and sampling speed, outperforming existing solvers like EM and PC.
Future Research Directions
Based on the proposed method, I believe that below approaches could be a possible further research direction.
-
Conditional Graph Generation Extending the framework to support property or topology conditioned generation would broaden its utility in drug discovery, materials design, and graph-based reasoning.
-
Learning with Hard Constraints Incorporating domain-specific constraints, like chemical valency rules, as projection steps or within constraint-aware score functions could significantly improve the validity of generated graphs.
-
Dynamic and Temporal Graphs Extending to dynamic graph generation, where both node features and edges evolve over time, would benefit applications such as interaction networks, financial systems, and physical simulations
-
Latent Diffusion for Graphs Considering latent diffusion models such as Stable Diffusion
, I think that exploring generating graphs in a learned latent space could be another exiting research approach to improve efficiency without sacrificing fidelity. -
Multimodal Graph Generation Graphs often co-occur with other modalities in scientific or social domain, in forms such as text and images. Designing joint diffusion frameworks for cross-modal graph generation could be another possible research direction.
$$
Extending GDSS: Latent Diffusion for Graphs
In this section, I outline a potential extension of GDSS, inspired by recent advances in latent diffusion models such as Stable Diffusion
One promising direction for scaling GDSS is to adapt its reverse-time SDE framework to operate in a latent space, rather than directly on full-resolution graphs. This could be a valid approach since the latent formulation has been effective in other domains for reducing computational cost while preserving high generative fidelity.
We can design the latent diffusion framework for graphs with the following components:
-
Graph Encoder
\[capturing both topological and semantic information.\]
A permutation-invariant encoder, such as a GNN with hierarchical pooling, maps each graph \(G = (X, A)\) to a compact latent vector $$ z \in \mathbb{R}^d, -
Latent Diffusion Process
\[to reverse the noising process and generate new latent vectors by simulating reverse-time dynamics.\]
A continuous-time SDE is applied in the latent space. The model learns a score function $$ s_{\psi,t}(z) -
Graph Decoder
A decoder reconstructs graph structures from latent representations, possibly using a graph-based VAE, graph transformer, or autoregressive generator conditioned on \(z.\)
This latent-GDSS architecture offers several advantages:
- Efficiency: Operating in the latent space reduces the dimensionality of the generative modeling problem, lowering training and sampling cost.
- Regularization: The encoder-decoder structure encourages a more structured, semantically meaningful manifold, improving generalization.
- Modality Compatibility: A shared latent space can enable multimodal extensions, such as text-to-graph generation or property-conditioned synthesis.
However, a core challenge is ensuring that the latent space remains sufficiently smooth and expressive to support stable diffusion modeling. This could be addressed through contrastive pretraining, joint training with score-based regularization, or denoising objectives that align with the graph decoder.
Enjoy Reading This Article?
Here are some more articles you might like to read next: