Exploring Chemical Space with Score-based Out-of-distribution Generation

Score-based generative models have shown promise in molecule generation, but often struggle to create truly novel candidates beyond the training distribution. MOOD (Molecular Out-Of-distribution Diffusion) is a score-based diffusion framework that enables controllable exploration of out-of-distribution chemical space without incurring additional computational costs. By integrating a property prediction network into the reverse-time SDE, MOOD effectively guides the generation toward molecules with desired novel traits such as high binding affinity, drug-likeness, and synthesizability.

Introduction: The Challenge of Novel Molecule Generation

In de novo drug discovery, deep generative models have emerged as powerful tools for automating the design of novel molecules. However, the generated molecules tend to closely resemble those in the training distribution, restricting their usefulness in discovering truly novel compounds with superior therapeutic potential. This is especially problematic when aiming to avoid patented scaffolds or explore uncharted regions of the chemical space. Moreover, real-world drug design often requires satisfying multiple complex property constraints, such as high binding affinity, drug-likeness, and synthesizability. Most existing models optimize simplistic proxy scores, which often result in trivial or unrealistic structures. This blog introduces MOOD (Molecular Out-Of-distribution Diffusion), a novel score-based generative framework that addresses these limitations by enabling controlled exploration beyond the training data, while optimizing for multiple drug-relevant properties.

Limitations of Existing Models

Prior works for molecular generation, such as VAE , GANs , and reinforcement learning-based models , primarily rely on learning distributions from existing molecular datasets. As a result, they exhibit a strong inductive bias toward the training distribution. For example, the molecules generated by GENTRL frequently exhibit strong resemblance to known active compounds. Some works attempt to explore novelty through fragment-based RL or prioritized replay, but these methods are still constrained by the fragments derived from known molecules and incur high computational costs. Even recent diffusion models like GDSS, while capable of generating high-quality molecular graphs, lack the mechanism to explicitly control the deviation from training data. Furthermore, these models often optimize over simplified properties (e.g., penalized logP, QED) that do not necessarily correlate with real-world drug efficacy.

MOOD: A New Paradigm for Out-of-Distribution Generation

Figure 1: Concept Figure of MOOD.

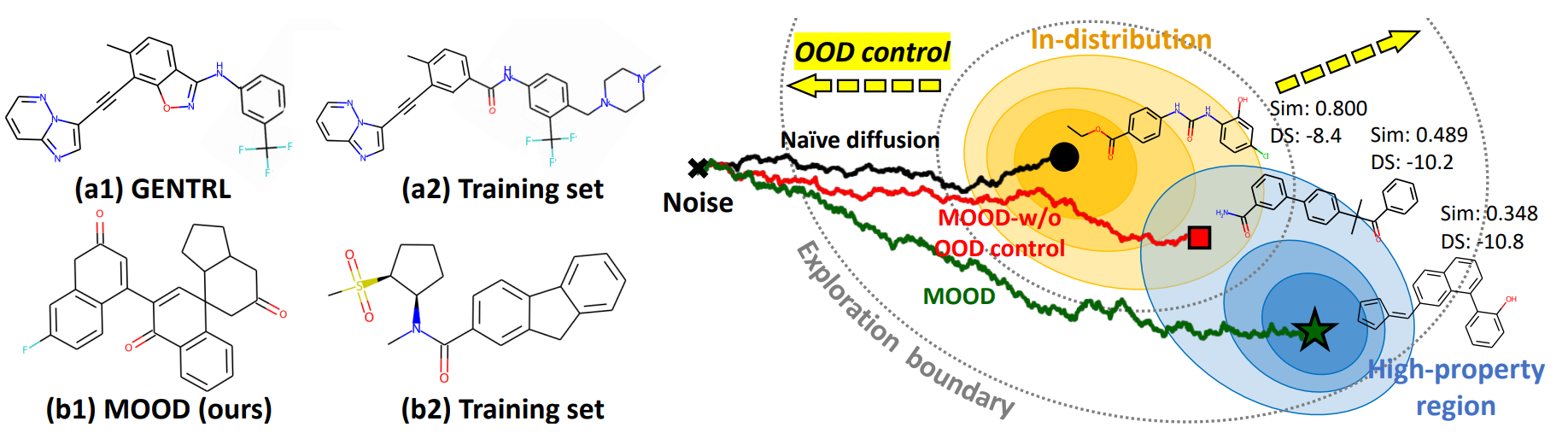
MOOD introduces a new framework for molecule generation that targets two fundamental challenges: (1) generating molecules that are truly novel and out-of-distribution (OOD), and (2) ensuring that these molecules satisfy real-world drug-like properties. For this, MOOD combines a novel OOD-controlled reverse-time diffusion process with gradient-based guidance from a property predictor. The OOD control mechanism allows fine-grained tuning of how far the generative process can deviate from the data distribution using a simple hyperparameter $\lambda$, while the property predictor guides the sampling toward regions in chemical space where molecules exhibit desired characteristics. Importantly, MOOD achieves this without relying on reinforcement learning or fragment vocabularies, and without incurring additional training or inference costs.

Score-based Generative Modeling with SDEs

In order to model the complex dependency between the nodes and edges, MOOD builds upon GDSS, a framework that models the diffusion process of molecular graphs via a system of stochastic differential equations (More details can be found in Blog Post “Score-based Generative Modeling of Graphs via the System of Stochastic Differential Equations”).

Therefore, the forward diffusion process is described by:

\[dG_t = f_t(G_t)\,dt + g_t\,d\omega\]

where $G_t = (X_t, A_t)$ is the molecular graph at time $t$, $f_t$ is the drift coefficient, $g_t$ is the scalar diffusion coefficient, and $\omega$ is a standard Wiener process.

The reverse-time diffusion process is given by:

\[\begin{aligned} dX_t &= \left[ f_{1,t}(X_t) - g_{1,t}^2 \nabla_{X_t} \log p_t(X_t, A_t) \right]dt + g_{1,t} d\bar{\omega}_1, \\\\ dA_t &= \left[ f_{2,t}(A_t) - g_{2,t}^2 \nabla_{A_t} \log p_t(X_t, A_t) \right]dt + g_{2,t} d\bar{\omega}_2, \end{aligned}\]

where $s_{\theta_1,t}$ and $s_{\theta_2,t}$ are score networks trained to approximate $\nabla_{X_t} \log p_t(X_t, A_t)$ and $\nabla_{A_t} \log p_t(X_t, A_t)$, respectively. The reverse-time SDEs are guided by learned score networks that approximate the gradient of the data distribution.

From GDSS to MOOD: Modeling Graphs via Joint SDEs

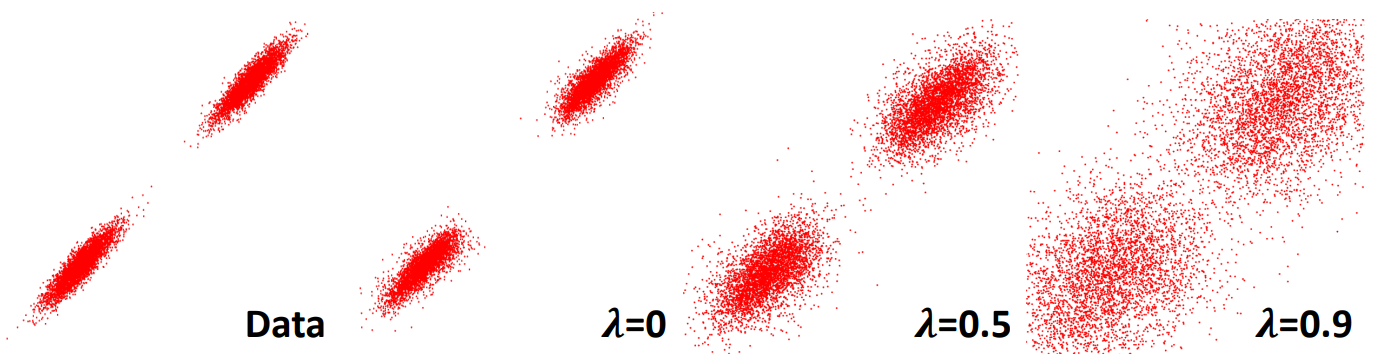
To enable OOD generation, MOOD modifies the reverse-time SDE with an additional drift term derived from the assumption that low-likelihood samples are more likely to be OOD. This is done by reweighting the generative distribution to emphasize lower-density areas, so MOOD defines the conditional distribution as follows:

\[p_t(G_t \mid y_o = \lambda) \propto p_t(G_t)^{1 - \sqrt{\lambda}},\]

where $y_0 = \lambda$ is a control variable indicating the degree of OOD-ness and $\lambda \in [0, 1)$. As shown in the equation, higher $\lambda$ encourages sampling from low-likelihood regions, which indicates more novel regions of the chemical space.

Therefore, the resulting OOD-controlled reverse-time SDE is given as:

\[dG_t = \left[ f_t(G_t) - (1 - \sqrt{\lambda}) g_t^2 \nabla_{G_t} \log p_t(G_t) \right] dt + g_t d\bar{\omega},\]

where \(f_t(G_t)\) is the drift, \(g_t\) is the diffusion scale, and \(d\bar{\omega}\) is the reverse-time Wiener process. When \(\lambda=0\) , this reduces to the standard score-based SDE. Further analysis regarding the effect of $\lambda$ is shown in Figure 2.

Figure 2: A toy experiment on the OOD-controlled diffusion.

Conditional Generation for Property Optimization

MOOD further refines generation to favor molecules with desirable chemical properties using conditional generation. Here, the objective is to sample from the joint conditional distribution:

\[p_t(G_t \mid y_o = \lambda, y_p),\]

where $y_p$ represents a property condition such as high binding affinity, drug-likeness. This is decomposed using Bayes’ rule:

\[p_t(G_t \mid y_o = \lambda, y_p) \propto p_t(G_t) \, p_t(y_o = \lambda \mid G_t) \, p_t(y_p \mid G_t, y_o = \lambda).\]

The property term \(p_t(y_p \mid G_t, y_o = \lambda)\) is modeled with a Boltzmann distribution:

\[p_t(y_p \mid G_t, y_o = \lambda) = \frac{1}{Z_t} \exp\left( \alpha_t P_\phi(G_t, \lambda) \right),\]

where $P_\phi$ is a learned property prediction function and $\alpha_t$ is a scaling parameter. Substituting this into the reverse-time SDE gives:

\[dG_t = \left[ f_t(G_t) - (1 - \sqrt{\lambda}) g_t^2 \nabla_{G_t} \log p_t(G_t) - \alpha_t g_t^2 \nabla_{G_t} P_\phi(G_t, \lambda) \right] dt + g_t d\bar{\omega},\]

where the last term encourages sampling toward regions with higher predicted property values.

Therefore, following the form of GDSS, this can be seperated into node features $X_t$ and adjacency matrix $A_t$ as below:

\[\begin{aligned} dX_t &= \left[ f_{1,t}(X_t) - (1 - \sqrt{\lambda}) g_{1,t}^2 s_{\theta_1,t}(X_t, A_t) - \alpha_{1,t} g_{1,t}^2 \nabla_{X_t} P_\phi(X_t, A_t, \lambda) \right] dt + g_{1,t} d\bar{\omega}_1, \\ dA_t &= \left[ f_{2,t}(A_t) - (1 - \sqrt{\lambda}) g_{2,t}^2 s_{\theta_2,t}(X_t, A_t) - \alpha_{2,t} g_{2,t}^2 \nabla_{A_t} P_\phi(X_t, A_t, \lambda) \right] dt + g_{2,t} d\bar{\omega}_2, \end{aligned}\]

where $s_{\theta_1,t}$ and $s_{\theta_2,t}$ are score networks approximating the partial derivatives of the log data density with respect to $X_t$ and $A_t$, respectively.

To balance the influence of the score and property gradients, MOOD dynamically adjusts the weighting coefficients:

\[\alpha_{1,t} = \frac{r_{1,t} \| s_{\theta_1,t}(G_t) \|}{\| \nabla_{X_t} P_\phi(G_t, \lambda) \|}, \quad \alpha_{2,t} = \frac{r_{2,t} \| s_{\theta_2,t}(G_t) \|}{\| \nabla_{A_t} P_\phi(G_t, \lambda) \|},\]

where $r_{1,t}$ and $r_{2,t}$ are manually defined scaling ratios. This ensures that the property optimization does not overpower or vanish relative to the diffusion guidance.

As a result, by focusing on OOD generation and property optimization, MOOD enables both controlled exploration and the generation of chemically meaningful molecules.

Experimental Results

Novel Molecule Generation

To evaluate MOOD’s ability to generate truly novel molecules, expriment was conducted in unconstrained OOD generation task, so generating molecules without explicitly optimizing for chemical properties. The goal is to validate whether MOOD’s $\lambda$-controlled diffusion process can produce molecules that systematically deviate from the training data distribution. Trained on ZINC250k dataset, MOOD generates 3000 molecules using different values of $\lambda$, with the property optimized term $P_\phi$ removed. The following metrics are used to evaluate the novelty and diversity of the generated molecules:

Figure 3: (Left) UMAP visualization of the ZINC250k dataset and the generated molecules by the proposed OOD-controlled diffusion process. (Right) Evaluation results of the molecules generated by the OOD-controlled diffusion.

As shown in Figure 3 (a)-(d), increasing λ causes the samples to diverge farther from the training data in the latent space. This visually confirms that MOOD’s OOD-controlled diffusion process offers smooth and tunable control over novelty.

Moreover, in the right side of Figure 3, both FCD and NSPDK MMD increase monotonically with λ, suggesting greater divergence in biochemical features and molecular graph structures. The novelty also increases, meaning the generated molecules are not only different in distribution but also chemically unique at the molecular level.

Therefore, these results demonstrate that MOOD can generate molecules in a controlled and data-driven manner that generalizes beyond the training distribution—opening doors to the exploration of novel chemical space.

Property Optimization

To evaluate whether MOOD can discover compounds that are not only out-of-distribution (OOD) but also biochemically optimal, such as high binding affinity, strong drug-likeness, and good synthetic accessibility, experiment regarding practical demands of real-world de novo drug discovery has been conducted.

To reflect multi-objective optimization, the following commposite property function has been defined:

\[P_{\text{obj}}(G_t) = \text{DS'}(G_t) \times \text{QED}(G_t) \times \text{SA'}(G_t)\]

where

A neural property predictor $P_\phi$ is trained on molecules from the ZINC250k dataset to learn $P_{\text{obj}}$. To evaluate performance, joint measures of novelty and property optimization have been conducted as follows:

To test the generality, the evaluations are performed across five protein targets, parp1, fa7, 5ht1b, braf, and jak2, with OOD control strength is fixed at $\lambda = 0.04$.

Table 1: Novel hit ratio (%) results.
Table 2: Novel top 5% docking score (kcal/mol) results.

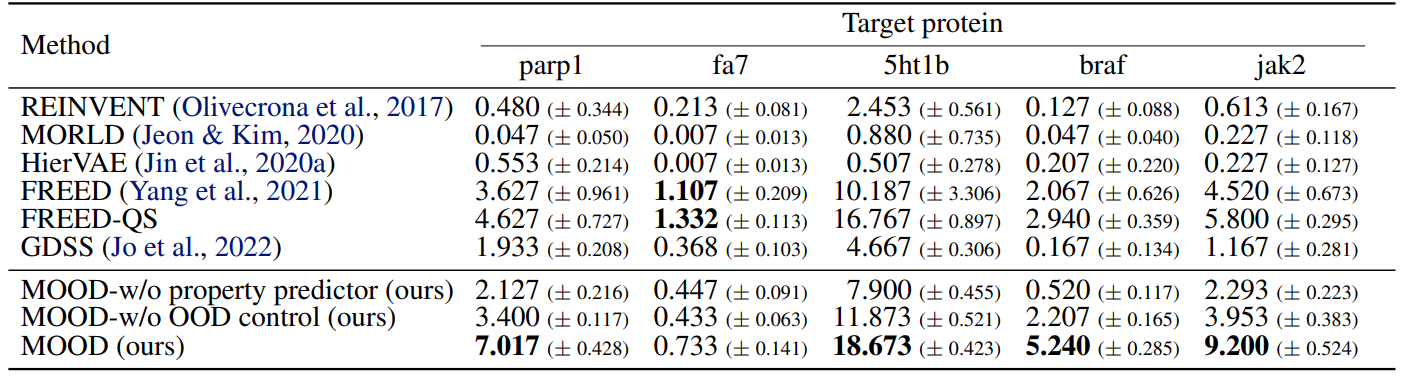
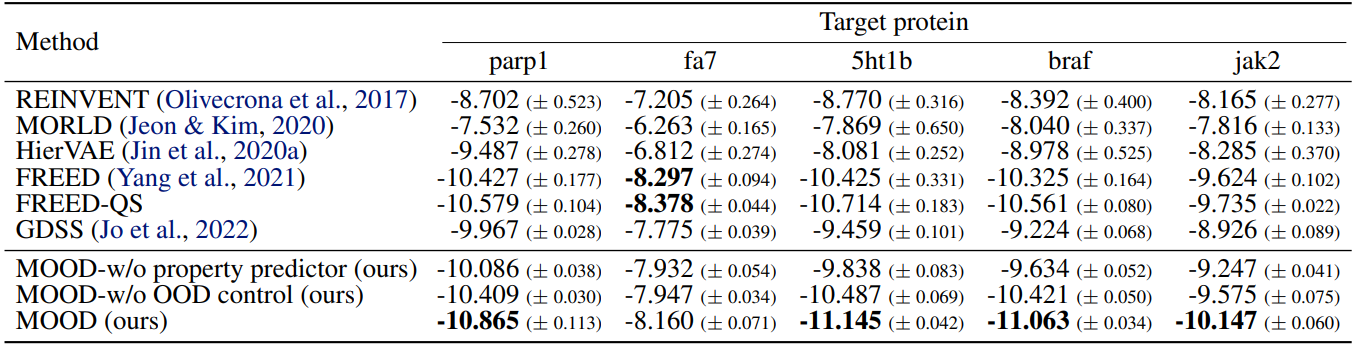
As shown in Tables 1, 2, MOOD achieves state-of-the-art performance across almost all protein targets.

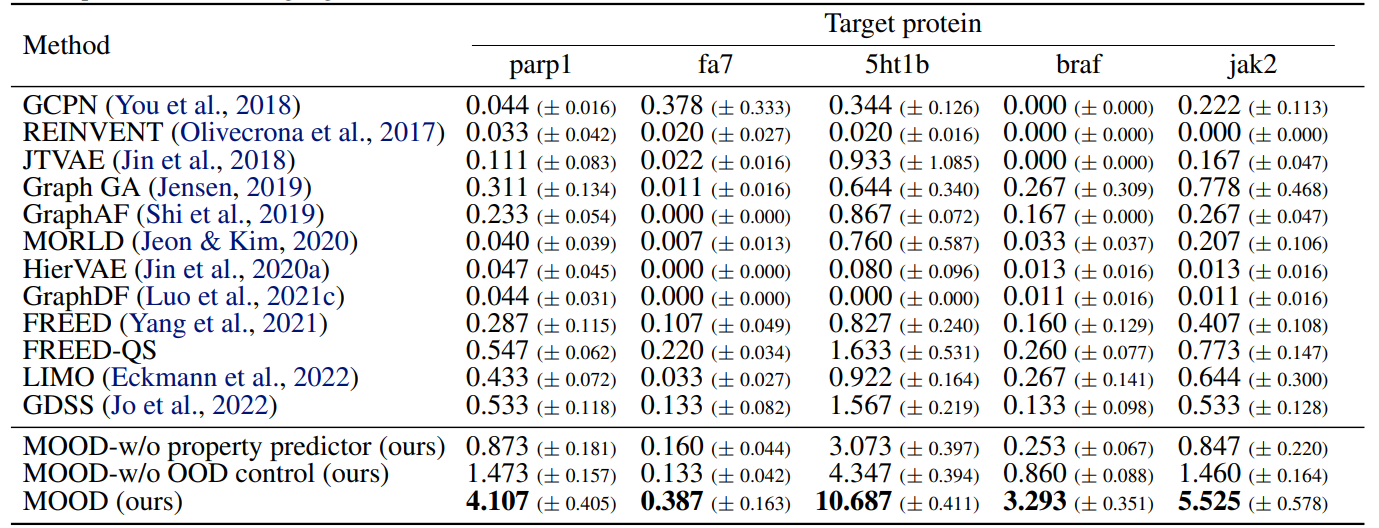
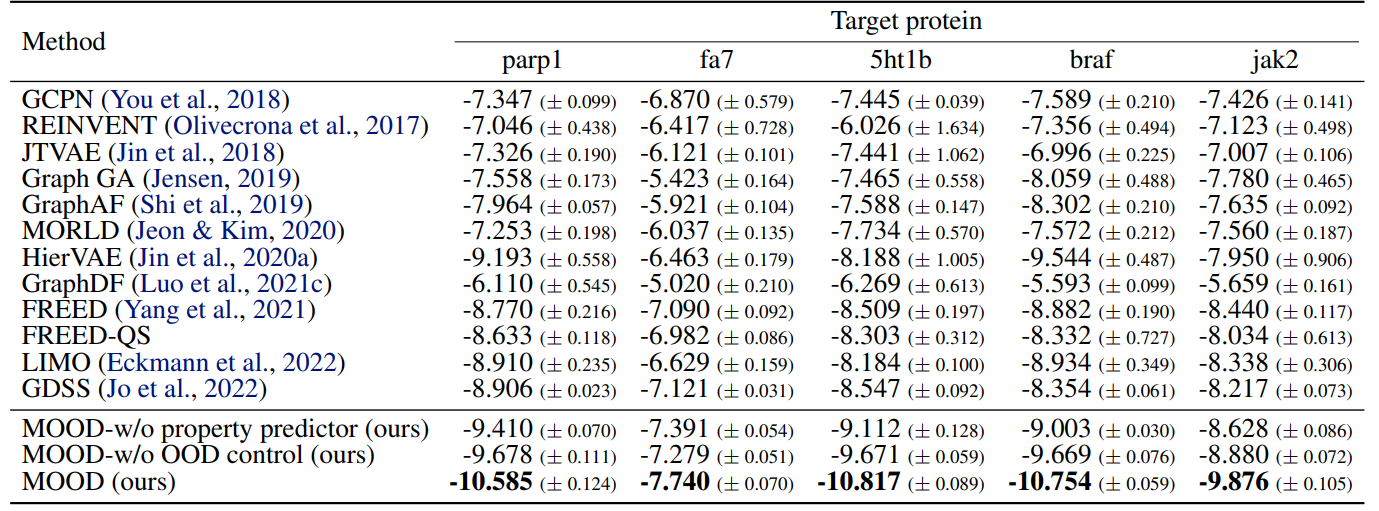
Table 3: Novel hit ratio (%) results with the similarity condition of 0.3.
Table 4: Novel top 5% docking score (kcal/mol) results with the similarity condition of 0.3.

Moreover, it outperforms all baselines in novel hit ratio and top-5% docking scores, especially under stricter novelty thresholds (Tables 3, 4).

Especially, MOOD consistently beats MOOD-w/o OOD control, which proves that $\lambda$-based exploration improves discovery. But MOOD-w/o property predictor still outperforms GDSS, showing that the OOD mechanism alone adds significant value.

Further results in the Appendix (Table 9-13) of the paper shows that MOOD also maintains high uniqueness, broad structural diversity, and robust hit rates.

These findings suggest that MOOD’s balanced guidance allows it to find chemically diverse and viable compounds that elude conventional methods.

Explorability Visualization

Figure 4: (Left) UMAP visualization of the molecules from ZINC250k and the generated samples with parp1 as the target protein. (Right) Distributional distances of the generated molecules measured by FCD and NSPDK MMD with respect to ZINC250k.

UMAP visualization (Figure 4, Left) shows that MOOD explores chemical space more broadly than competitors like REINVENT and FREED-QS, whose outputs cluster near the training data.
MOOD’s samples visibly shift into new, unexplored regions, showing the role of the OOD term.

Metrics such as FCD and NSPDK MMD (Figure 4, Right) further demonstrates this distributional divergence.

Generated Molecules and Visual Inspection

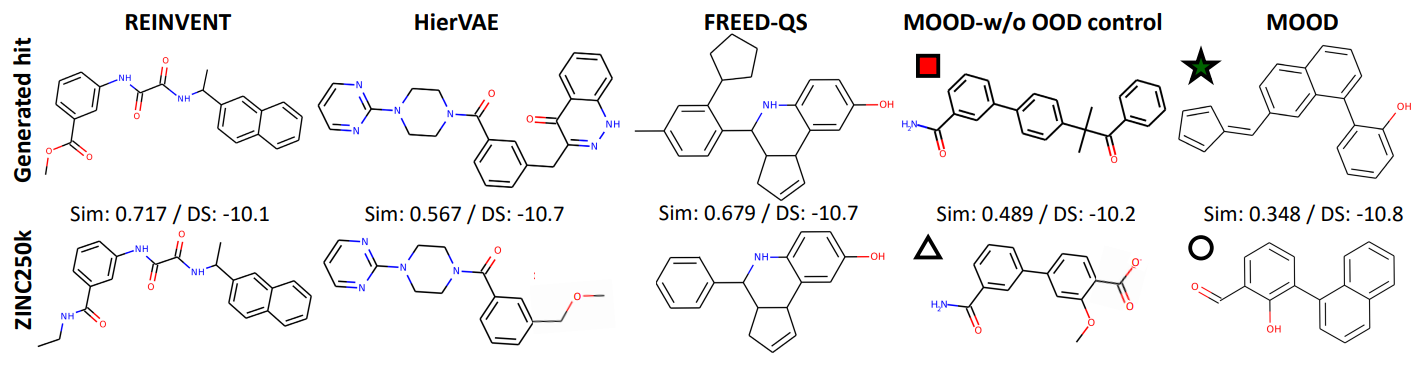
Figure 5: Generated hit molecules with parp1 as the target protein and the corresponding ZINC250k molecules of the highest similarity.

Figures 5 compares the actual molecules produced by each method, and this shows that the baseline models tend to reproduce redundant motifs or slight variations of training data. On the other hand, MOOD’s molecules reveal low similarity to ZINC250k yet high binding affinity, demonstrating the novelty and utility.

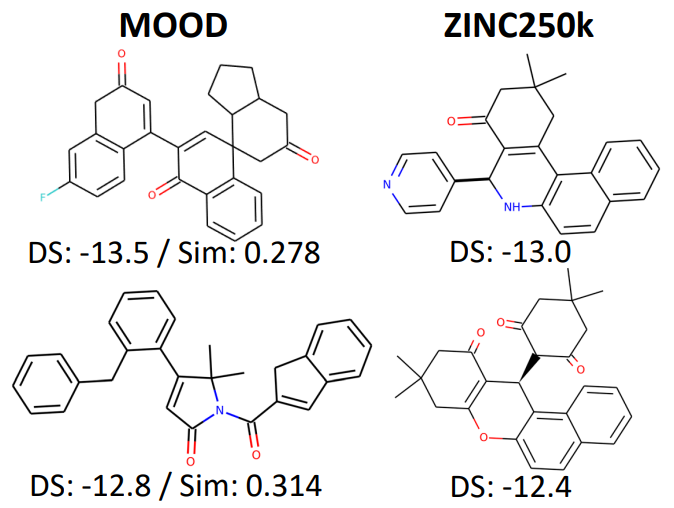
Figure 6: Novel hit molecules found by MOOD against parp1 and the top 0.01% ZINC250k molecules.

Furthermore, Figure 6 highlights MOOD’s hits that outperform the top 0.01% of ZINC250k molecules in docking score while remaining dissimilar, underscoring MOOD’s effectiveness in discovering novel chemical optima.

Comparison to 3D Generation Models

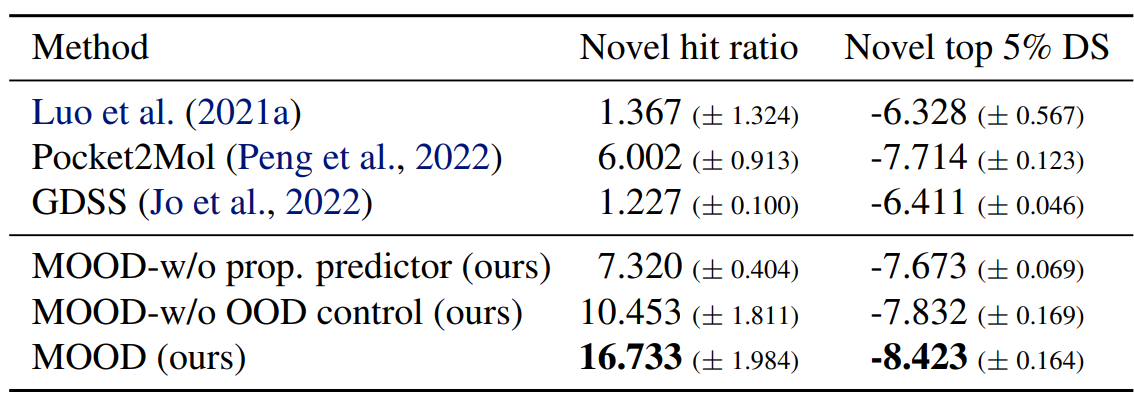
Table 5: Novel hit ratio (%) and novel top 5% docking score (kcal/mol) results with 3D molecule generation baselines and GDSS with respect to the target protein glmu.

MOOD is also benchmarked against modern 3D molecule generation models, such as Luo et al. and Pocket2Mol, which leverages spatial binding site data. The result in Table 5 shows that MOOD outperforms both, even though it does not use any 3D information, emphasizing its practicality and generalization strength.

Ablation Studies

To isolate the contributions of each core component in MOOD, the authors perform a comprehensive ablation study. This analysis investigates how both the OOD control mechanism and the property-guided gradient contribute to the quality and novelty of generated molecules.

Effects of OOD Control and Property Gradient

To understand the effect of each module, the following variants are compared: (1) MOOD-w/o Property Predictor, which disables property conditioning, keeping OOD guidance only (2) MOOD-w/o OOD Control, which disables $\lambda$-based novelty control, using only the property gradient (3) GDSS: baseline diffusion model without OOD or property guidance (4) Full MOOD, which combines both OOD control and property optimization.

As shown in Tables 1–3, both OOD control and property optimization are necessary for achieving the best chemical optima, and this can be explained as:

Training on Low-Property Subsets: Can MOOD Discover What It Never Saw?

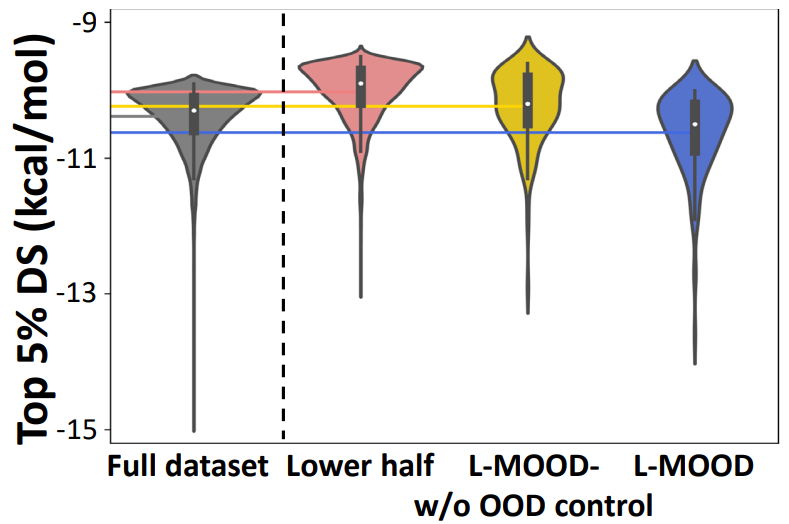
Figure 7: Top 5% docking score distribution of the molecules with respect to the target protein parp1.

To test MOOD’s ability to generalize beyond biased training data, the following model variants are trained on a low-quality subset of the ZINC250k dataset (bottom 50% ranked by $P_{\text{obj}}$): (1) L-MOOD-w/o OOD Control, which is trained only with property guidance (2) L-MOOD, which is trained with both OOD control and property guidance. The top 5% docking scores (DS) is evaluated for generated molecules that satisfy QED > 0.5 and SA < 5. As shown in Figure 7, both L-MOOD and L-MOOD-w/o OOD Control outperform their low-quality training data, proving the effectiveness of property-based diffusion. Only L-MOOD surpasses the full ZINC250k dataset in top-5% DS, despite never seeing high-quality molecules during training. This shows that OOD-controlled diffusion not only fosters novelty but can also find superior optima in property space, effectively extrapolating beyond the limits of training data.

Final Thoughts

MOOD addresses the core limitation of molecular graph generation with the ability to explore novel chemical spaces while optimizing for real-world drug-like properties.

By integrating OOD-controlled reverse-time diffusion with property-guided gradient optimization, MOOD creates a principled and controllable pathway for discovering molecules that are both chemically novel and pharmacologically relevant.

Key Takeaways

Further Research Directions

Based on the proposed method, I believe that below approaches could be a possible further research direction.

Extending MOOD: Incorporating 3D Structural Information

In this section, I propose a potential extension of MOOD by integrating 3D structural information of target proteins into the generative process. While MOOD currently operates only in the 2D topological space of molecules, ligand–protein interactions are fundamentally 3D, and incorporating spatial constraints from protein binding pockets can improve biological relevance.

The 3D-aware MOOD framework could be designed as follows:

  1. Protein Pocket Encoder
    A neural encoder processes the 3D structure of a protein binding site, represented as a voxel grid, surface mesh, or point cloud, to produce a latent descriptor $$ p \in \mathbb{R}^d,

    \[capturing shape and electrochemical features relevant for binding.\]

  2. Conditioned Property Predictor
    The property prediction network \(P_\phi(G_t, \lambda)\) is augmented to incorporate protein context as $$ P_\phi(G_t, \lambda, p),

    \[allowing MOOD to optimize molecules for both chemical properties and spatial compatibility with the target site.\]

  3. Modified Reverse-Time SDE
    The conditional diffusion process is updated to guide generation with both OOD control and protein-specific gradients:

    \[dG_t = \left[ f_t(G_t) - (1 - \sqrt{\lambda}) g_t^2 \nabla_{G_t} \log p_t(G_t) - \alpha_t g_t^2 \nabla_{G_t} P_\phi(G_t, \lambda, p) \right] dt + g_t d\bar{\omega}.\]

This protein-aware extension of MOOD offers several advantages:

Possible issues such as the limited availability of aligned protein–ligand datasets and the increased complexity of modeling in 3D can be mitigated using transfer learning from structural databases such as PDBbind, or by leveraging pretrained protein encoders like those used in AlphaFold2 or EquiBind.

Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • Score-based Generative Modeling of Graphs via the System of Stochastic Differential Equations