CS.30707
(2025S, 7th Semester, KAIST) Intro to Reinforcement Learning - Vectorized Reward-based Attribution for Interpretable Learning
VRAIL: Vectorized Reward-based Attribution for Interpretable Learning [arXiv] [code] [slide]
- course instructor: Prof. Sungjin Ahn
- authors: Jina Kim, Youjin Jang, Jeongjin Han (equal contribution)
- affiliations: KAIST, South Korea
Overview
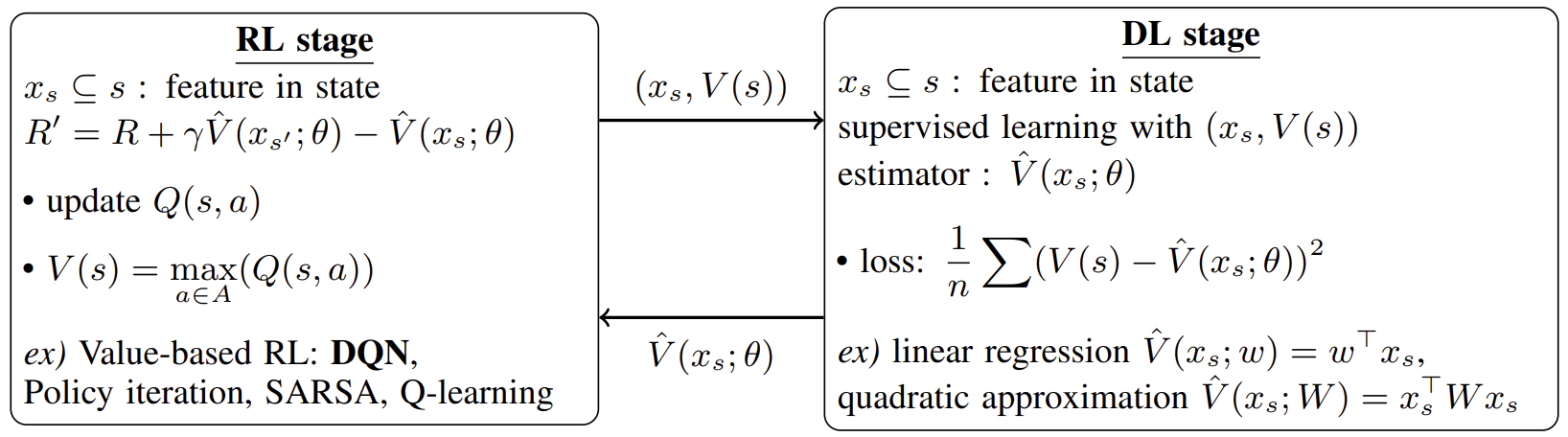
We propose VRAIL (Vectorized Reward-based Attribution for Interpretable Learning), a bi-level framework for value-based reinforcement learning (RL) that learns interpretable weight representations from state features.
VRAIL consists of two stages:
- a deep learning (DL) stage that fits an estimated value function using state features, and
- an RL stage that uses this to shape learning via potential-based reward transformations.
The estimator is modeled in either linear or quadratic form, allowing attribution of importance to individual features and their interactions. Empirical results on the Taxi-v3 environment demonstrate that VRAIL improves training stability and convergence compared to standard DQN, without requiring environment modifications. Further analysis shows that VRAIL uncovers semantically meaningful subgoals (such as passenger possession), highlighting its ability to produce human-interpretable behavior. Our findings suggest that VRAIL serves as a general, model-agnostic framework for reward shaping that enhances both learning and interpretability.
Motivation
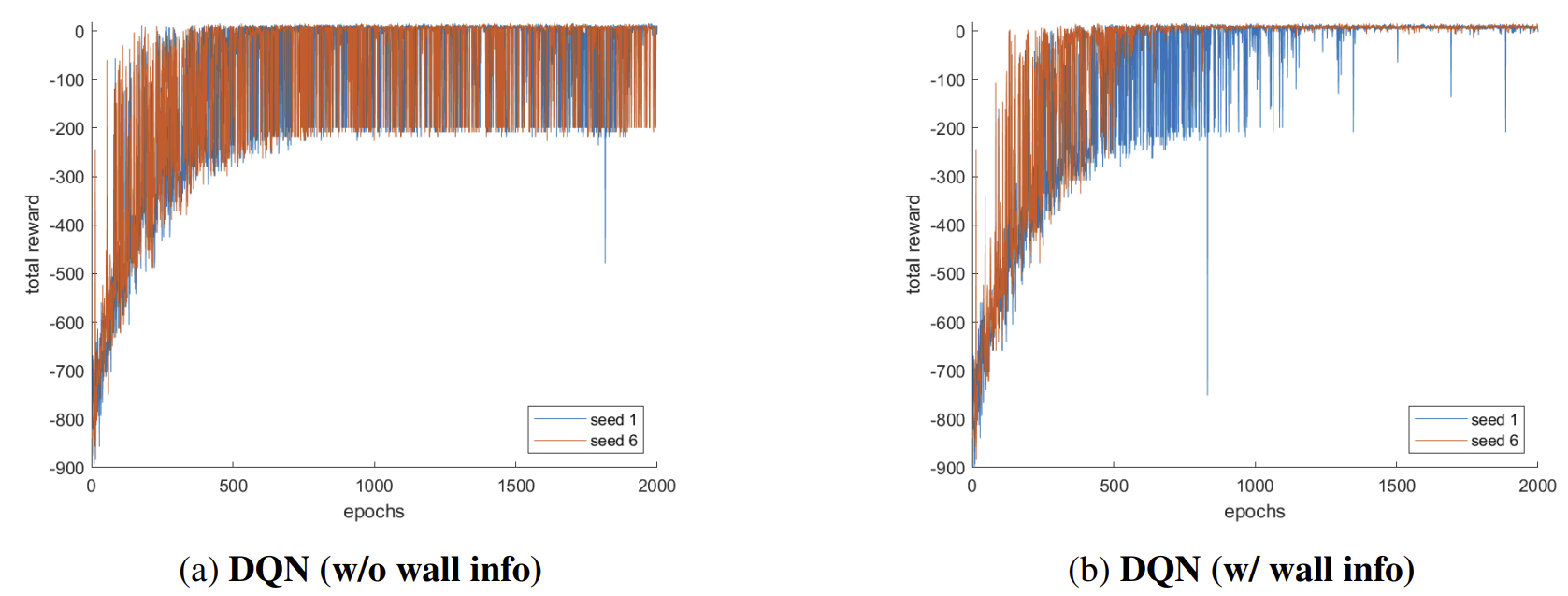
In reinforcement learning, agents often struggle when state representations are incomplete or reward signals are sparse/delayed.
For example, in the Taxi-v3 environment:
- The default state space lacks wall information, which is crucial for successful navigation.
- A vanilla DQN baseline sometimes fails to converge (2 out of 10 runs).
- When wall information is manually added, DQN converges consistently — but such interventions are impractical in real-world settings.
VRAIL addresses this challenge by learning feature-based reward shaping functions that uncover latent subgoals (e.g., “passenger is in taxi”), stabilizing training without modifying the environment.
Key Features
-
Bi-level Optimization:
- RL Stage: Learns policies with shaped rewards.
- DL Stage: Fits an interpretable value function from state features (linear or quadratic).
- Interpretability: Produces weight vectors and feature interactions that highlight important factors in decision-making.
- Training Stability: More robust convergence compared to vanilla DQN.
- Model-Agnostic: Can be applied to value-based RL methods (DQN, SARSA, Q-learning, etc.).
- Generalizable Reward Shaping: Learned shaping functions can be transferred to other agents.
Method Overview
VRAIL alternates between two stages:
-
RL Stage
Reward shaping with a potential function:R'(s, a, s') = R(s, a, s') + γ V̂(x_{s'}; θ) − V̂(x_s; θ)- Uses any value-based RL algorithm (e.g., DQN).
- Encourages intermediate progress toward the final goal.
-
DL Stage
Learns interpretable value functions:-
Linear VRAIL:
V̂(x_s; w) = wᵀ x_s -
Quadratic VRAIL:
V̂(x_s; W) = x_sᵀ W x_s - Attributes importance to features and feature interactions.
-
Linear VRAIL:
This forms a closed-loop bi-level optimization between RL and DL stages.
Experiments
- Environment: Taxi-v3 (Gymnasium)
- Baselines: Compared against vanilla DQN.
-
Results:
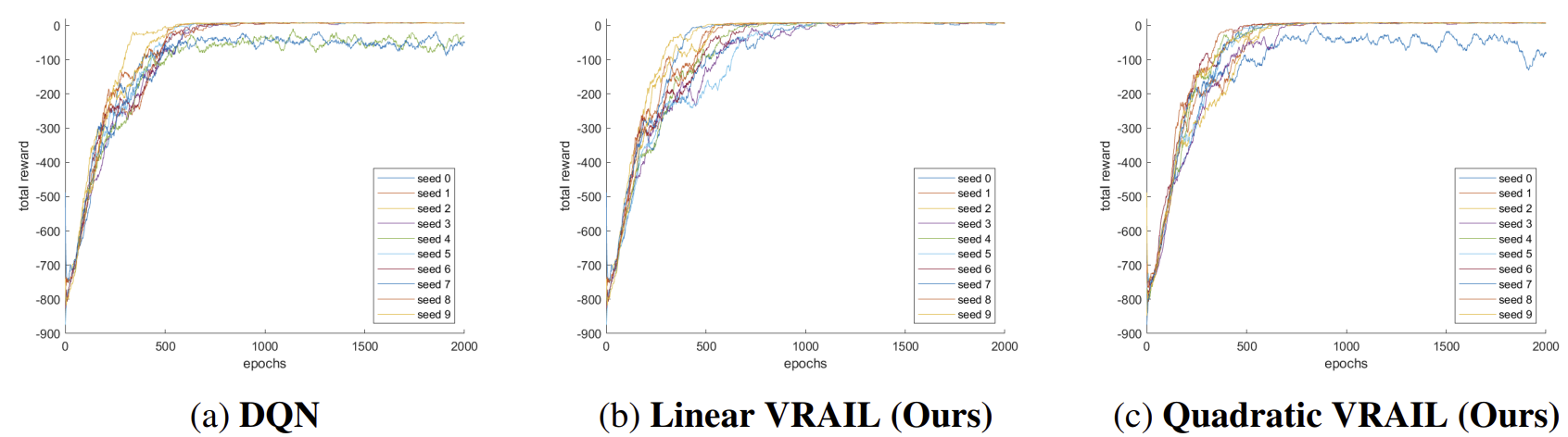
- Linear VRAIL: Highest robustness (converged in 10/10 seeds).
- Quadratic VRAIL: Fastest convergence speed.
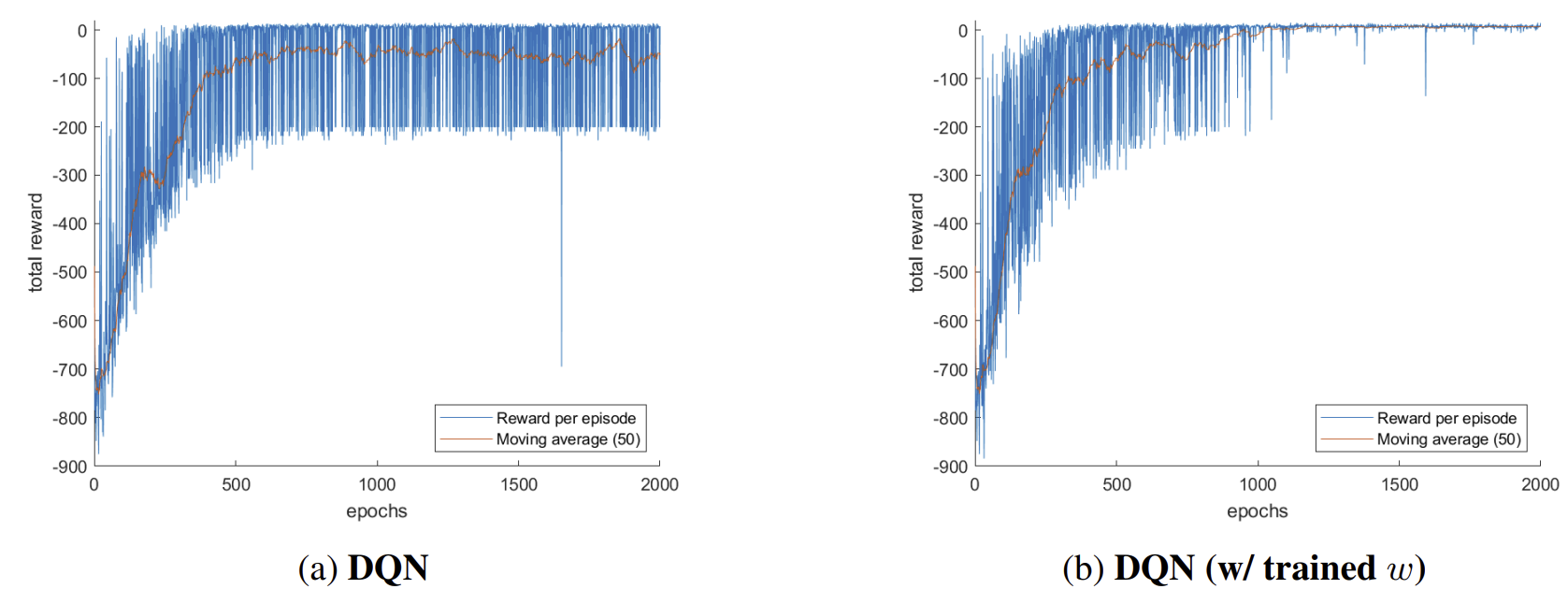
- Transferability: Pretrained VRAIL reward functions improve vanilla DQN convergence.
Example Findings:
- Linear VRAIL learns that “Passenger in Taxi” is the most important subgoal.
- Quadratic VRAIL highlights feature interactions between location, passenger, and destination.
Results
- Linear VRAIL: Most stable (converged in all runs), but slightly slower.
- Quadratic VRAIL: Faster convergence and highly robust, though not as perfectly stable as Linear.
1. Training Stability Comparison Across Models
- VRAIL improves convergence robustness compared to DQN:
- DQN: 8/10 runs
- Linear VRAIL: 10/10 runs
- Quadratic VRAIL: 9/10 runs
2. Average epochs to reach reward thresholds (10 seeds, excluding top/bottom 2 outliers)
| Reward Threshold | DQN | Linear VRAIL | Quadratic VRAIL |
|---|---|---|---|
| -10 | 600.00 | 614.17 | 538.17 |
| -5 | 612.17 | 643.17 | 562.83 |
| 0 | 648.17 | 652.50 | 594.33 |
| +5 | 717.67 | 735.83 | 660.17 |
3. Effect of Reward Shaping Using a Pretrained Linear VRAIL Model
A pretrained Linear VRAIL shaping function, when transferred to DQN, improves stability and eliminates non-converging runs.
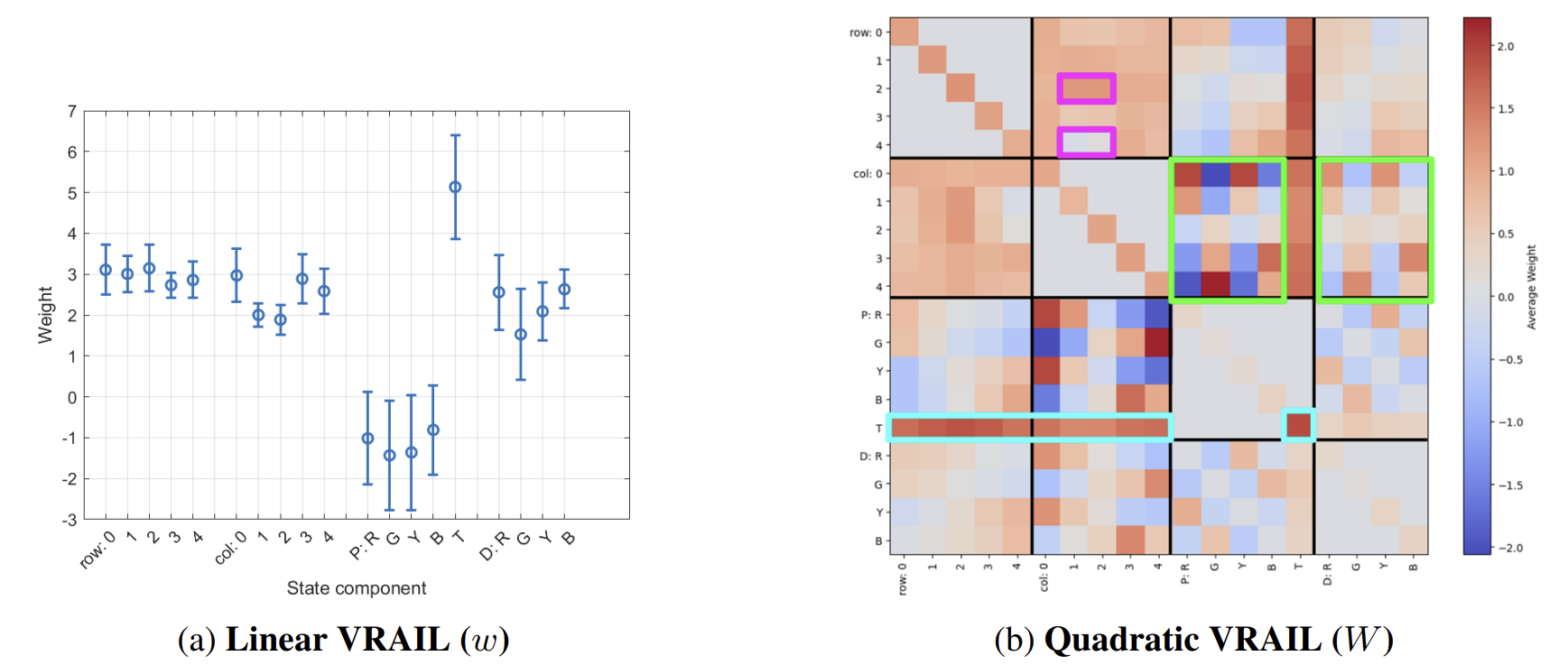
Visualization of Learned Parameters of DL Stage
- Linear VRAIL: Feature weights highlight passenger possession as the most important subgoal.
- Quadratic VRAIL: Heatmap of pairwise feature interactions shows strong coupling between passenger and destination features.
Team Contributions
All team members actively contributed to every stage of the project, including project concretization, trials for method improvement, slides, and report writing. Further individual contributions are detailed below.
- Jina Kim : Backbone model implementation (Linear VRAIL), DQN toy experiment (Fig 1), self-attention based model trials, final refinement of the report.
- Youjin Jang : Idea proposal (vectorized rewards), presentation, quiz creation, visualization (graphs, diagrams).
- Jeongjin Han : Interpretation of learned parameters of DL stage, effect of shaped reward experiment (Fig 4), α-scheduling trials, environment variants trials.
Citation
@misc{kim2025vrailvectorizedrewardbasedattribution,
title={VRAIL: Vectorized Reward-based Attribution for Interpretable Learning},
author={Jina Kim and Youjin Jang and Jeongjin Han},
year={2025},
eprint={2506.16014},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2506.16014},
}